采用蒙特卡羅(MC)技術，研究了液體不飽和一維非均質多孔介質中兩相（水和油）流動的行為。在確定性a和隨機log-k、完全相關log-k和a、統計無關（不相關）log-k和a過程的條件下，在分析中使用了兩個空間相關的隨機過程，即本征滲透率、k和土壤保持參數a。用龍格庫塔法計算毛細管壓力。本研究的結果用于預測兩相流動由于相互依賴的穩定水和油流量的定性行為，以及輸入隨機過程的規定組合。結果表明，滲透率、k和土壤保持性a的空間變異性對于預測流動行為的重要性。

介紹

有機污染物在地下的運動通常涉及水、非水相液體(NAPL)或俗稱的“油”，以及三流相多孔介質中的蒸汽。傳統的多相流數值模擬涉及在每個有代表性的地下地層中假定恒定的地下性質(Osborne&Sykes，1986年；Kaluarachchi&Parker，1989年；Kaluarachchi等人，1990年)然而，在過去十年中，地下水水文學家證明，在給定的地層中的異質性及其空間結構影響飽和和不飽和狀態下的有效流動特性(Yeh等人，1985年a，1985年b；Mantoglou&Gelhar，1987年a，1987年b；Kemblowski&Chang，1993年)。與非飽和和飽和流動相似，可以假定烴類污染地下的多相流也受局部尺度地下非均質性的影響。Abdin等人最近進行的一項研究。（1994年）和Chang等人。（1994)表明，液體飽和介質中的兩相(水和油）流動受土壤滲透性和土壤保持參數的空間變異性的顯著影響。

本研究的目的是擴展Abdin等人的工作。（1994）利用蒙特卡羅(MC)技術研究液體-不飽和非均相介質的多相流動行為。輸入隨機過程是本征滲透率、k和土壤保持參數a。通過研究氣油和油水毛細壓力的變化規律，分析了流動行為。

理論

假設一個靜態氣相，不可壓縮水中的油氣流動和等溫多孔介質可以用兩個耦合的非線性流動方程描述為

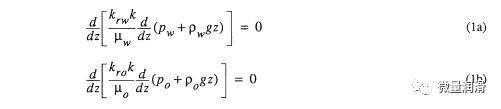
其中pp是p相密度(p=w，水；p=o，油；p是a，空氣)；krp是相對導水率；k是多孔介質的本征滲透率；\ip是流體動態粘度；p“是流體壓力；z是垂直高程坐標；g是重力引起的加速度。由于土體本構關系的非線性，控制方程(La)和(Lb)是耦合的，高度非線性的。通常假定流體對固體基質的潤濕性或親和力從空氣、油到水相增加，毛細管壓力是潤濕流體飽和度的函數。在本研究中，有兩種流體界面：（1)油水界面；(2）由于液體不飽和條件而產生的氣油界面。因此，水飽和度是油水毛細管壓力的函數，總液飽和度是空氣油毛細管壓力的函數。

在此分析中，我們考慮了一個簡單的指數參數模型來描述壓力-飽和度-滲透率關系。因此，該系統的相對相位電導率可以寫成

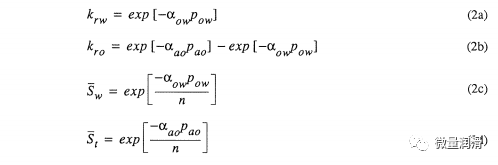
式中，pow（=p0 pw）為油水毛細管壓力；pao（=pa-p0）為氣油毛細管壓力；aow（=a（3olv）和aao（=a$ao）為取決于土壤類型和流體對的參數；~SW為有效含水飽和度；S為有效總液體飽和度（含水飽和度和含油飽和度之和）；是曲線擬合參數。這里a是土壤滯留參數，Povv和（3ao）是僅取決于有機污染物的流體標度參數。

利用朗格-庫塔法得到了耦合方程和lb方程的解。在該方法中，得到了表示從下表面開始的單個滯后距離的每個土層的解。利用跨層壓力的連續性，依次得到了整個高度的解。所使用的邊界條件是規定的流體通量和下表面的1型條件。規定了這些邊界條件，以使整個柱的總液體飽和度保持得小于1。這種條件允許存在兩個流體界面，油水和空氣油。控制流方程的解產生了波w和泡o的漸近行為，因為氣體壓力pa被假設是一個常數，我們也得到了個別壓力p0和pw的漸近解。

輸入過程的隨機表示

分析中考慮的輸入隨機過程是空間相關的內在滲透率k（f=對數）和土壤保持參數a。這些參數被假設為二階平穩隨機過程，并呈正態分布。在模擬中使用的三種不同的輸入隨機過程的組合是

（1）完全相關。 

（2）隨機/過程和確定性a，

（3）統計獨立或不相關/和a。

模擬中使用的“空穴”自協方差函數Rg和相應的譜Sg

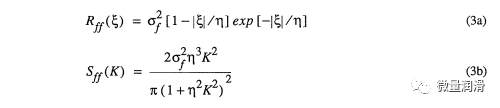
其中，£是滯后距離，rj是相關尺度，oy是/的標準差，K是波數。使用葉等人所描述的光譜方法進行了隨機生成。（1985年a）

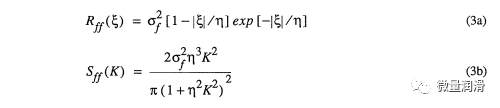
其中X(Z)是隨機隨機過程；A/是離散化頻率=0/M；[-0，0]是SffK)不重要的頻率范圍；M是該范圍內離散頻率的總數；/t‘=/t8/；0/是A/‘«A/«A/»時在范圍內均勻分布的頻率[-0.5A/»，0.5A/»，/*。=(AT-0.5)A/；§k是均勻分布在[0，2JI]范圍內的獨立隨機角]。

使用延（1989）概述的程序獲得了統計上獨立的/和一個分布。通過對互相關函數的分析，驗證了這兩個參數之間的統計依賴性的程度。

示例模擬

進行了一些模擬，以評估關鍵輸入土壤性質的空間變異性對流動行為的影響。流域由1000厘米長的垂直土柱組成。流域離散為1000層，每層1cm。這里考慮的有機流體是相對密度為0.8的輕烴。其中，i0，n，$ow和(3^的值分別為0.0065g cm“1s”1、11.2.183和2.2。平均/，平均a，oy和aa分別為-18.3，1.366x10厘米，0.5和1.336x10厘米。空間相關長度為25cm，基數分別為-10cm和-10cm。水和油在下表面的1型邊界條件分別為10和1.1x10gcm1。規定的水和油通量使介質通過柱保持液體不飽和(ST<。

 結果與討論

在本節中，我們給出了不同的模擬的結果，以了解關鍵的地下特性的空間變異性對兩相流的影響。

所規定的個別流體通量的影響

預先形成了兩組模擬，以評估改變給定相位規定的流體通量對毛細管壓力和飽和度的整體行為的影響。在每一組中，一個給定的流體的基殼通量發生了改變，而剩余的流體通量則保持了恒定。隨機輸入過程/和a也通過線性關系完全相關（阿丁等人，1994）。假設遍歷假設有效的單一模擬結果表明（是的，1989）。

與水通量從10“5”到10“7cms”1的變化相關的模擬結果如圖1(a)、1(b)、2(a)和2(b)所示。圖1(a)和1(b)中的結果顯示了沿圓柱的毛細管壓力分布。我們觀察到，隨著水通量，qw從107增加到105厘米1，pw的變異性下降，而p^的相應變異性增加。這些結果在物理上是合理的，因為隨著水通量的增加，含水的飽和度和^也會增加（見方程式2(a)）。

根據Yeh（1989）的非飽和流分析和Abdin等人（1994）的多相流分析結果，由于潤濕流體飽和度的增加，pow的可變性應減小。圖1（b）中給出的pao（z）分布的行為與pow的行為相反，在pow中，我們觀察到平均pao略微降低以適應增加的Sw。該行為表明S的變化最小（見等式2（d））。因此，如圖2（b）所示，我們觀察到沿著域的平均S0減小，以適應更高的平均S。此外，由于Pao的變異性隨著qw的增加而增加，因此St的變異性也應該增加。St和Sw之間的變異性變化產生了圖2（b）所示的S0的變異性，在圖中我們觀察到隨著qw的增加，因此表現出減少的變異性。

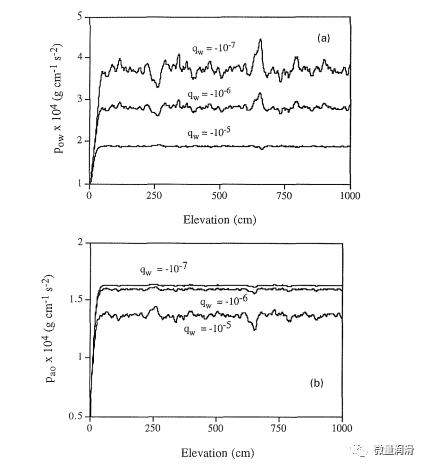
圖1    油通量恒定在10“5厘米s”1時，不同水通量沿土壤柱的毛細管壓力分布；(A)油-水毛細管壓力和(B)氣-油毛細管壓力。

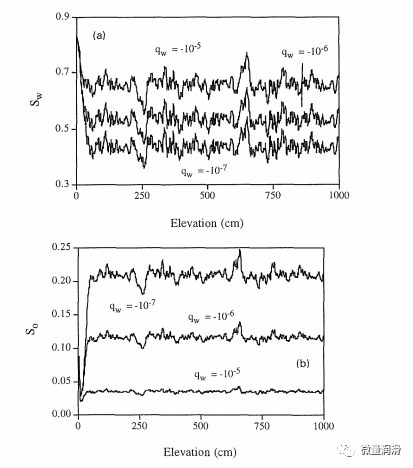
圖2當油通量為10“5”時，不同水通量下土壤柱上的流體飽和度分布cm s“1；（a）含水飽和度和（b）含油飽和度。

圖3(A)和圖3(B)中的結果顯示了由于Q0從10“6”到10“4cms”1的變化而導致PAO和S0的變異性，而QW保持在基值。結果表明，PaO(Z)行為具有鏡像效應，在<7O=10“5cms”1‘時，變異性幾乎可以忽略不計。這種行為類似于Yeh（1989）在不飽和流動中觀察到的行為。在前面的結果討論中，我們沒有觀察到這種行為，因為規定的QW范圍可能不包括這個臨界值。圖3(B)顯示，隨著Q0的增加，S0的變異性增加，平均S0增加，以適應較高的油通量。

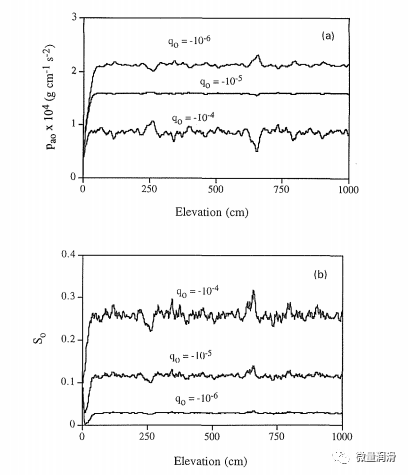
圖3當水通量為10~6cms*1時，不同油通量下的毛管壓力和飽和度沿土柱的分布；（a）氣油毛管壓力；（b）含油飽和度。

深度統計分析

在本節中，我們建議研究輸入隨機過程的不同組合對毛細管壓力變化的影響。圖4中的結果顯示了pow opow的標準偏差，該偏差是使用基本情況參數對各種輸入隨機組合進行的50次蒙特卡羅模擬計算得出的。這些結果表明，當輸入組合從完全相關的，確定性的a變為統計上未修正的情況時，平均opow依次增加。結果表明，在任意深度下，pow的最小變異性是由完全相關的logfc得到的，而當兩個參數在統計上不相關時，pow的最大變異性是由logfc得到的。圖5（a）和圖5（b）顯示了p^，apao的可變性。在這里，我們也觀察到pœ在任何深度的變異性在統計上不相關的情況下較高，而在完全相關的情況下最低。在每種情況下，由于地下性質的隨機變化，沿區域的毛細壓力變化是高度隨機的。我們還觀察到，在所有三種情況下，opao的平均值遠小于opow的平均值。同樣對于<spow和opao，確定性和統計上不相關的情況之間的值更接近，因為相應的完全相關的情況值要小得多。因此，可以得出結論，如果有必要，只考慮完全相關和統計獨立的情況，可以簡化這三種組合。

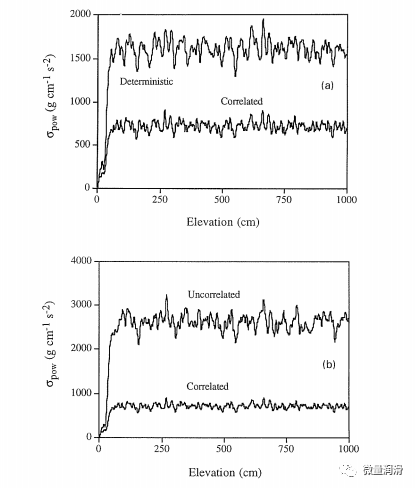
圖4通過50個蒙特卡羅模擬計算的沿土柱的油水毛管壓力（apow）的變化：（a）相關與確定性a，（b）相關與統計獨立（不相關情況）情況。

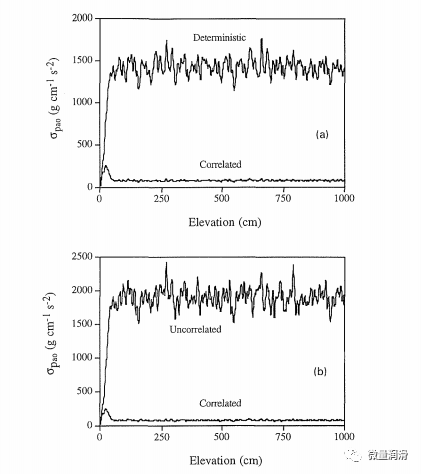
圖5根據50個蒙特卡羅模擬計算的沿土柱的氣-油毛管壓力（opao）變化；（a）相關與確定性a，以及（b）相關與統計獨立（不相關情況）情況。

結論

本文的目的是利用montecarlo方法研究非均質多孔介質中油水兩相流動的隨機行為。模擬結果表明，當任一相的穩態流量發生變化時，相應的平均毛管壓力和飽和度也發生變化。此外，根據流體流量的變化，沿剖面的飽和度和毛管壓力的變化也可能在兩種流動流體之間以耦合方式發生變化。毛管壓力在任意深度的變化對描述地下性質的輸入隨機過程高度敏感。在任何深度上，完全相關情況下的毛管壓力變化比確定性或完全不相關情況下的變化小得多。總之，這項工作的結果證明了在研究兩相流行為時考慮關鍵地下性質的空間變異性的重要性。